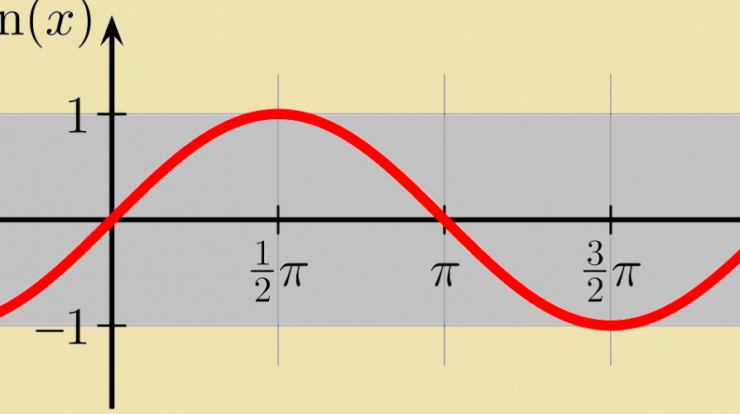
Sine definition – Delving into the enigmatic world of trigonometry, we encounter the sine function, a mathematical concept that holds immense significance in shaping our understanding of angles, waves, and periodic motion. Defined as the ratio of the opposite side to the hypotenuse in a right triangle, the sine function unveils a treasure trove of applications that extend far beyond the realm of geometry.

Throughout this exploration, we will unravel the intricate relationship between sine and cosine, delve into its practical applications in trigonometry, calculus, and physics, and uncover the captivating ways in which it illuminates the world around us.

Sine Definition and Basic Properties

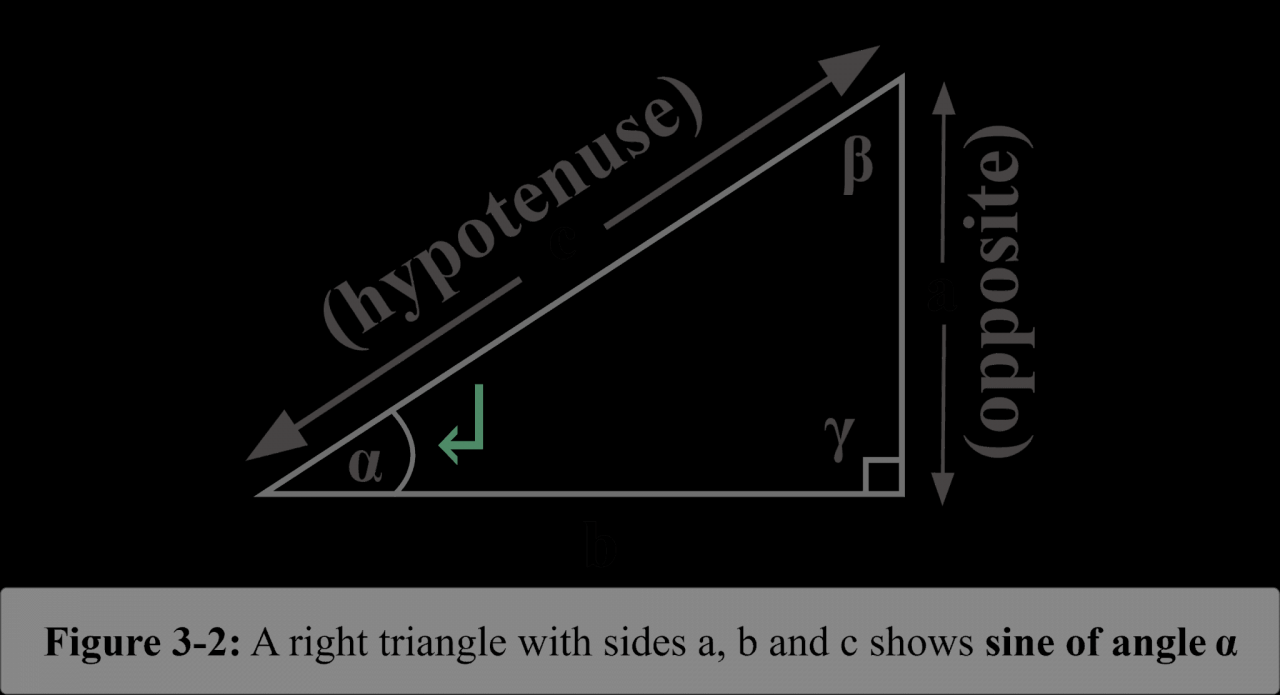
The sine function is a trigonometric function that describes the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle. It is denoted by the abbreviation “sin”.

The range of the sine function is [-1, 1], and its period is 2π. The sine function is an odd function, meaning that it is symmetric about the origin.

The sine function is related to the cosine function by the identity sin^2(x) + cos^2(x) = 1.

Applications in Trigonometry

• Finding the height of a tower or building using the sine function.
• Solving problems involving angles and distances using the sine function.
• Examples of real-world applications of sine in trigonometry include surveying, navigation, and astronomy.

Applications in Calculus, Sine definition

• Finding the derivative and integral of a function using the sine function.
• The relationship between sine and the derivative of cosine.
• Examples of how sine is used in calculus problems include finding the velocity and acceleration of an object moving in a circular path.

Applications in Physics

• Modeling periodic motion, such as a pendulum or a vibrating spring, using the sine function.
• Analyzing sound waves and other types of waves using the sine function.
• Examples of how sine is used in physics applications include acoustics, optics, and mechanics.

Outcome Summary

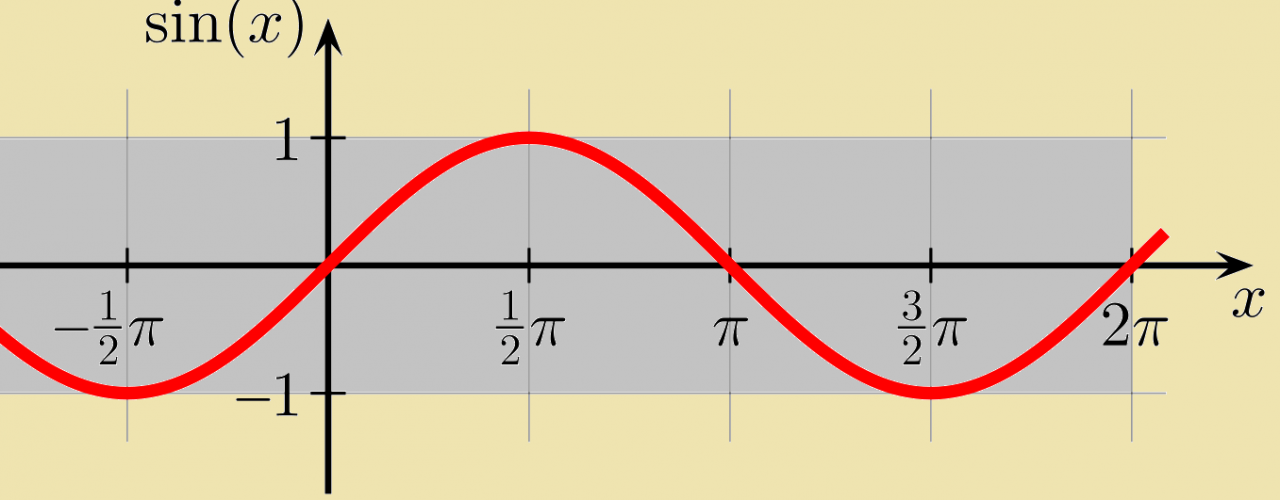
In conclusion, the sine function stands as a cornerstone of mathematical exploration, providing a versatile tool for unraveling the mysteries of angles, distances, and periodic phenomena. Its applications span a vast array of disciplines, from trigonometry and calculus to physics and engineering, making it an indispensable concept in our quest to understand the complexities of our universe.

Expert Answers

What is the range of the sine function?

The range of the sine function is [-1, 1].

What is the period of the sine function?

The period of the sine function is 2π.

How is sine used to find the height of a tower?

Sine can be used to find the height of a tower by measuring the angle of elevation from a known distance.